Algorytm Dijkstry

Algorytm Dijkstry, opracowany przez holenderskiego informatyka Edsgera Dijkstrę, służy do znajdowania najkrótszej ścieżki z pojedynczego źródła w grafie o nieujemnych wagach krawędzi.

Algorytm Dijkstry

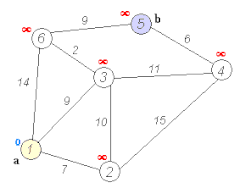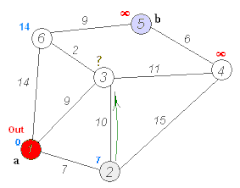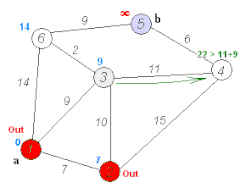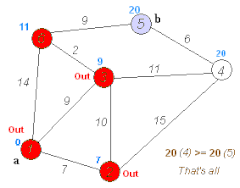Ilustracja działania algorytmu
Rodzaj	Znajdowanie najkrótszej ścieżki
Struktura danych	graf
Złożoność
Czasowa	$O(E\cdot \log V)$
Pamięciowa	$O(E+V\cdot \log V)$ - przy użyciu kopca Fibonacciego

Działanie

Mając dany graf z wyróżnionym wierzchołkiem (źródłem) algorytm znajduje odległości od źródła do wszystkich pozostałych wierzchołków. Łatwo zmodyfikować go tak, aby szukał wyłącznie (najkrótszej) ścieżki do jednego ustalonego wierzchołka, po prostu przerywając działanie w momencie dojścia do wierzchołka docelowego, bądź transponując tablicę incydencji grafu.

Algorytm Dijkstry znajduje w grafie wszystkie najkrótsze ścieżki pomiędzy wybranym wierzchołkiem a wszystkimi pozostałymi, przy okazji wyliczając również koszt przejścia każdej z tych ścieżek.

Algorytm Dijkstry jest przykładem algorytmu zachłannego.

Algorytm

Przez $s$ oznaczamy wierzchołek źródłowy, $w(i,j)$ to waga krawędzi $(i,j)$ w grafie.

• Stwórz tablicę $d$ odległości od źródła dla wszystkich wierzchołków grafu. Na początku $d[s]=0,$ zaś $d[v]=\infty$ dla wszystkich pozostałych wierzchołków.
• Utwórz kolejkę priorytetową $Q$ wszystkich wierzchołków grafu. Priorytetem kolejki jest aktualnie wyliczona odległość od wierzchołka źródłowego $s.$
• Dopóki kolejka nie jest pusta:
  • Usuń z kolejki wierzchołek $u$ o najniższym priorytecie (wierzchołek najbliższy źródła, który nie został jeszcze rozważony)
  • Dla każdego sąsiada $v$ wierzchołka $u$ dokonaj relaksacji poprzez $u{:}$ jeśli $d[u]+w(u,v)<d[v]$ (poprzez $u$ da się dojść do $v$ szybciej niż dotychczasową ścieżką), to $d[v]:=d[u]+w(u,v).$

Na końcu tablica $d$ zawiera najkrótsze odległości do wszystkich wierzchołków.

Dodatkowo możemy w tablicy poprzednik przechowywać dla każdego wierzchołka numer jego bezpośredniego poprzednika na najkrótszej ścieżce, co pozwoli na odtworzenie pełnej ścieżki od źródła do każdego wierzchołka – przy każdej relaksacji w ostatnim punkcie $u$ staje się poprzednikiem $v.$

Zastosowanie

Z algorytmu Dijkstry można skorzystać przy obliczaniu najkrótszej drogi do danej miejscowości. Wystarczy przyjąć, że każdy z punktów skrzyżowań dróg to jeden z wierzchołków grafu, a odległości między punktami to wagi krawędzi.

Jest często używany w sieciach komputerowych, np. przy trasowaniu (przykładowo w protokole OSPF).

Pseudokod

Dijkstra(G,w,s):
   dla każdego wierzchołka v w V[G] wykonaj
      d[v] := nieskończoność
      poprzednik[v] := niezdefiniowane
   d[s] := 0
   Q := V
   dopóki Q niepuste wykonaj
      u := Zdejmij_Min(Q)
      dla każdego wierzchołka v – sąsiada u wykonaj
         jeżeli d[v] > d[u] + w(u, v) to
            d[v] := d[u] + w(u, v)
            poprzednik[v] := u

   Wyświetl("Droga wynosi: " + d[v])

Dowód poprawności

Oznaczmy przez $S$ zbiór wierzchołków, które zostały już zdjęte z kolejki. Dowód opiera się na następujących dwóch faktach (niezmiennikach), prawdziwych przez cały czas trwania algorytmu:

1. Dla każdego wierzchołka $v\in S,$ liczba $d[v]$ jest długością najkrótszej ścieżki od $s$ do $v.$
2. Dla każdego wierzchołka $v\notin S,$ $d[v]$ jest długością najkrótszej ścieżki do $v$ prowadzącej tylko przez wierzchołki z $S.$

Na początku oba fakty są oczywiste ($S$ jest zbiorem pustym). Przy zdejmowaniu wierzchołka $u$ z kolejki wiemy, na podstawie faktu 2, że nie da się do niego dojść żadną krótszą drogą przez wierzchołki z $S.$ Z drugiej strony, ponieważ $u$ ma najniższy priorytet, przejście przez jakikolwiek inny wierzchołek spoza $S$ dałoby od razu co najmniej tak samo długą ścieżkę. A zatem dołączając wierzchołek $u$ do $S,$ zachowujemy prawdziwość faktu 1. Następnie musimy uwzględnić fakt, że najkrótsza ścieżka do jakiegoś wierzchołka $v$ po wierzchołkach z nowego zbioru $S$ może teraz zawierać wierzchołek $u.$ Ale wtedy musi on być ostatnim na niej wierzchołkiem (do każdego innego dałoby się dojść krócej, nie używając $u$), a zatem jej długość równa jest $d[u]+w(u,v)$ i zostanie prawidłowo obliczona w następnym kroku algorytmu.

Złożoność

Złożoność obliczeniowa algorytmu Dijkstry zależy od liczby $V$ wierzchołków i $E$ krawędzi grafu. O rzędzie złożoności decyduje implementacja kolejki priorytetowej:

• wykorzystując „naiwną” implementację poprzez zwykłą tablicę, otrzymujemy algorytm o złożoności $O(V^{2})$
• w implementacji kolejki poprzez kopiec, złożoność wynosi $O(E\log V)$
• po zastąpieniu zwykłego kopca kopcem Fibonacciego złożoność zmienia się na $O(E+V\log V)$

Pierwszy wariant jest optymalny dla grafów gęstych (czyli jeśli $E=\Theta (V^{2})$), drugi jest szybszy dla grafów rzadkich $(E=\Theta (V)),$ trzeci jest bardzo rzadko używany ze względu na duży stopień skomplikowania i niewielki w porównaniu z nim zysk czasowy.

Problemy i algorytmy pokrewne

Algorytm Dijkstry nie działa, jeśli w grafie występują krawędzie z ujemnymi wagami – w tym wypadku używa się wolniejszego, lecz bardziej ogólnego algorytmu Bellmana-Forda. Jeśli graf nie jest ważony (wszystkie wagi mają wielkość 1), zamiast algorytmu Dijkstry wystarczy algorytm przeszukiwania grafu wszerz.

Algorytm A* jest pewnym uogólnieniem algorytmu Dijkstry, które pozwala przeszukiwać tylko część grafu, jednak wymaga dodatkowej wstępnej informacji (heurystyki) o odległościach wierzchołków.

Algorytm Prima znajdowania minimalnego drzewa rozpinającego oparty jest o bardzo podobny pomysł co algorytm Dijkstry.

Bibliografia

• E. W. Dijkstra: A note on two problems in connexion with graphs. In Numerische Mathematik, 1 (1959), S. 269–271.
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford Wprowadzenie do algorytmów, wyd. 7, WNT 2007, ISBN 83-204-3149-2.

Linki zewnętrzne

• Algorytm Dijkstry na wazniak.mimuw.edu.pl
• Implementacja w języku C++
• Animacja algorytmu Dijkstry. optlab-server.sce.carleton.ca. [zarchiwizowane z tego adresu (2014-12-20)].
• Przykład wykonania algorytmu Dijkstry krok po kroku