Zbiór dominujący
Zbiór dominujący (ang. Dominating set) grafu – taki podzbiór zbioru wierzchołków że każdy wierzchołek, który nie należy do ma w tym zbiorze co najmniej jednego sąsiada (jest połączony krawędzią z przynajmniej jednym wierzchołkiem z )[1].
Liczba dominowania (ang. Domination number) grafu – liczba wierzchołków w najmniejszym zbiorze dominującym grafu Liczba dominowania jest oznaczana jako [1].
Zbiór totalnie dominujący (ang. Total dominating set) grafu – taki zbiór dominujący w którym każdy wierzchołek z ma co najmniej jednego sąsiada w Oznacza to, że każdy wierzchołek z jest incydentalny do innego wierzchołka z [1].
Liczba totalnego dominowania (ang. Total domination number) grafu – liczba wierzchołków w najmniejszym zbiorze totalnie dominującym grafu Liczba totalnego dominowania jest oznaczana jako [1].
-
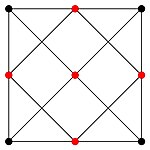
Przykładowy zbiór dominujący (nie totalnie) w grafie
-
Przykładowy zbiór totalnie dominujący w grafie
-
Najmniejszy zbiór dominujący (nie totalnie), liczba dominowania – 3
-
Najmniejszy zbiór totalnie dominujący, liczba totalnego dominowania – 3
Zobacz też
edytujPrzypisy
edytuj- ↑ a b c d Dominowanie w grafach. www.mif.pg.gda.pl. [dostęp 2015-12-14]. [zarchiwizowane z tego adresu (2015-12-22)].