Nierówność Jensena – nierówność między wartością funkcji wypukłej określonej dla kombinacji wypukłej pewnych argumentów a wypukłą kombinacją wartości funkcji w tych argumentach, przy czym obie kombinacje wypukłe mają te same współczynniki. Nazwa nierówności pochodzi od nazwiska Johana Jensena , duńskiego matematyka i inżyniera.
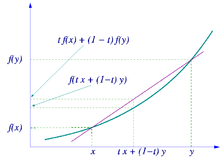
Nierówność Jensena przedstawiona graficznie
Dla dowolnych liczb
a
1
,
a
2
,
…
,
a
n
∈
[
0
,
1
]
,
{\displaystyle a_{1},a_{2},\dots ,a_{n}\in [0,1],}
wagami , spełniających warunek:
a
1
+
a
2
+
…
+
a
n
=
1
,
{\displaystyle a_{1}+a_{2}+\ldots +a_{n}=1,}
dla dowolnego przedziału
P
⊆
R
,
{\displaystyle P\subseteq \mathbb {R} ,}
x
1
,
x
2
,
…
,
x
n
∈
P
{\displaystyle x_{1},x_{2},\dots ,x_{n}\in P}
i dowolnej funkcji
f
{\displaystyle f}
wypukłej w
P
,
{\displaystyle P,}
[1]
f
(
∑
i
=
1
n
a
i
x
i
)
⩽
∑
i
=
1
n
a
i
f
(
x
i
)
.
{\displaystyle f\left(\sum _{i=1}^{n}a_{i}x_{i}\right)\leqslant \sum _{i=1}^{n}a_{i}f(x_{i}).}
Dla funkcji wklęsłych prawdziwa jest nierówność w przeciwną stronę.
Obrazkowy dowód nierówności Jensena. Punkt będący średnią ważoną punktów
(
x
i
,
φ
(
x
i
)
)
{\displaystyle (x_{i},\varphi (x_{i}))}
otoczce wypukłej , która (z wypukłości ) leży nad wykresem funkcji. Dowód indukcyjny ze względu na
n
.
{\displaystyle n.}
Dla
n
=
1
{\displaystyle n=1}
n
=
2
{\displaystyle n=2}
Niech
n
⩾
2.
{\displaystyle n\geqslant 2.}
f
(
∑
i
=
1
n
a
i
x
i
)
⩽
∑
i
=
1
n
a
i
f
(
x
i
)
,
{\displaystyle f\left(\sum _{i=1}^{n}a_{i}x_{i}\right)\leqslant \sum _{i=1}^{n}a_{i}f(x_{i}),}
gdzie
x
i
{\displaystyle x_{i}}
P
{\displaystyle P}
a
1
+
a
2
+
…
+
a
n
=
1.
{\displaystyle a_{1}+a_{2}+\ldots +a_{n}=1.}
Teza indukcyjna to:
f
(
∑
i
=
1
n
+
1
b
i
x
i
)
⩽
∑
i
=
1
n
+
1
b
i
f
(
x
i
)
,
{\displaystyle f\left(\sum _{i=1}^{n+1}b_{i}x_{i}\right)\leqslant \sum _{i=1}^{n+1}b_{i}f(x_{i}),}
gdzie
x
i
{\displaystyle x_{i}}
P
{\displaystyle P}
b
1
+
b
2
+
…
+
b
n
+
1
=
1.
{\displaystyle b_{1}+b_{2}+\ldots +b_{n+1}=1.}
Niech
x
i
∈
P
{\displaystyle x_{i}\in P}
b
1
+
b
2
+
…
+
b
n
+
1
=
1.
{\displaystyle b_{1}+b_{2}+\ldots +b_{n+1}=1.}
b
n
+
1
≠
0.
{\displaystyle b_{n+1}\neq 0.}
f
(
∑
i
=
1
n
+
1
b
i
x
i
)
=
f
(
b
1
x
1
+
⋯
+
b
n
+
1
x
n
+
1
)
=
{\displaystyle f\left(\sum _{i=1}^{n+1}b_{i}x_{i}\right)=f\left(b_{1}x_{1}+\dots +b_{n+1}x_{n+1}\right)=}
=
f
(
b
1
x
1
+
⋯
+
b
n
−
1
x
n
−
1
+
(
b
n
+
b
n
+
1
)
(
b
n
b
n
+
b
n
+
1
x
n
+
b
n
+
1
b
n
+
b
n
+
1
x
n
+
1
)
)
⩽
{\displaystyle =f\left(b_{1}x_{1}+\dots +b_{n-1}x_{n-1}+(b_{n}+b_{n+1})({\tfrac {b_{n}}{b_{n}+b_{n+1}}}x_{n}+{\tfrac {b_{n+1}}{b_{n}+b_{n+1}}}x_{n+1})\right)\leqslant }
Korzystając z założenia indukcyjnego:
⩽
b
1
f
(
x
1
)
+
⋯
+
b
n
−
1
f
(
x
n
−
1
)
+
(
b
n
+
b
n
+
1
)
f
(
b
n
b
n
+
b
n
+
1
x
n
+
b
n
+
1
b
n
+
b
n
+
1
x
n
+
1
)
⩽
{\displaystyle \leqslant b_{1}f(x_{1})+\dots +b_{n-1}f(x_{n-1})+(b_{n}+b_{n+1})f({\tfrac {b_{n}}{b_{n}+b_{n+1}}}x_{n}+{\tfrac {b_{n+1}}{b_{n}+b_{n+1}}}x_{n+1})\leqslant }
Z definicji funkcji wypukłej:
⩽
b
1
f
(
x
1
)
+
⋯
+
b
n
−
1
f
(
x
n
−
1
)
+
(
b
n
+
b
n
+
1
)
b
n
b
n
+
b
n
+
1
f
(
x
n
)
+
(
b
n
+
b
n
+
1
)
b
n
+
1
b
n
+
b
n
+
1
f
(
x
n
+
1
)
{\displaystyle \leqslant b_{1}f(x_{1})+\dots +b_{n-1}f(x_{n-1})+(b_{n}+b_{n+1}){\tfrac {b_{n}}{b_{n}+b_{n+1}}}f(x_{n})+(b_{n}+b_{n+1}){\tfrac {b_{n+1}}{b_{n}+b_{n+1}}}f(x_{n+1})}
=
b
1
f
(
x
1
)
+
⋯
+
b
n
−
1
f
(
x
n
−
1
)
+
b
n
f
(
x
n
)
+
b
n
+
1
f
(
x
n
+
1
)
=
∑
i
=
1
n
+
1
b
i
f
(
x
i
)
,
{\displaystyle =b_{1}f(x_{1})+\dots +b_{n-1}f(x_{n-1})+b_{n}f(x_{n})+b_{n+1}f(x_{n+1})=\sum _{i=1}^{n+1}b_{i}f(x_{i}),}
co kończy dowód.
Aby udowodnić nierówność gdy
f
{\displaystyle f}
−
f
{\displaystyle -f}
(
−
f
)
(
∑
i
=
1
n
a
i
x
i
)
⩽
∑
i
=
1
n
a
i
(
−
f
)
(
x
i
)
,
{\displaystyle (-f)\left(\sum _{i=1}^{n}a_{i}x_{i}\right)\leqslant \sum _{i=1}^{n}a_{i}(-f)(x_{i}),}
co jest równoważne nierówności
f
(
∑
i
=
1
n
a
i
x
i
)
⩾
∑
i
=
1
n
a
i
f
(
x
i
)
.
{\displaystyle f\left(\sum _{i=1}^{n}a_{i}x_{i}\right)\geqslant \sum _{i=1}^{n}a_{i}f(x_{i}).}
W szczególności dla
a
1
=
a
2
=
…
=
a
n
=
1
/
n
{\displaystyle a_{1}=a_{2}=\ldots =a_{n}=1/n}
f
(
∑
i
=
1
n
x
i
n
)
⩽
∑
i
=
1
n
f
(
x
i
)
n
.
{\displaystyle f\left({\frac {\sum _{i=1}^{n}x_{i}}{n}}\right)\leqslant {\frac {\sum _{i=1}^{n}f(x_{i})}{n}}.}
Korzystając z nierówności Jensena, można udowodnić dużą liczbę nierówności, na przykład nierówność między średnią arytmetyczną i geometryczną . Nierówność ma też wiele zastosowań w fizyce i rachunku prawdopodobieństwa .
edytuj
![{\displaystyle a_{1},a_{2},\dots ,a_{n}\in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74bdebccf001085565e9294ee73f6d0e5af2cbf3)
