Współczynnik korelacji Pearsona
Współczynnik korelacji liniowej Pearsona – współczynnik określający poziom zależności liniowej między zmiennymi losowymi. Został opracowany przez Karla Pearsona.
Wzory matematyczne
edytujNiech i będą zmiennymi losowymi o dyskretnych rozkładach. oznaczają wartości prób losowych tych zmiennych natomiast – wartości średnie z tych prób, tj.
Wówczas estymator współczynnika korelacji liniowej definiuje się następująco:
Ogólnie współczynnik korelacji liniowej dwóch zmiennych jest ilorazem kowariancji i iloczynu odchyleń standardowych tych zmiennych:
W szczególności dla zmiennych losowych o dyskretnych rozkładach ma on postać
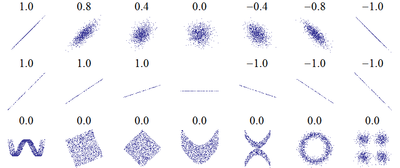
Wartość współczynnika korelacji mieści się w przedziale domkniętym [−1, 1]. Im większa jego wartość bezwzględna, tym silniejsza jest zależność liniowa między zmiennymi. oznacza brak liniowej zależności między cechami, oznacza dokładną dodatnią liniową zależność między cechami, natomiast oznacza dokładną ujemną liniową zależność między cechami, tzn. jeżeli zmienna rośnie, to maleje i na odwrót.
Współczynnik korelacji liniowej można traktować jako znormalizowaną kowariancję. Korelacja przyjmuje zawsze wartości w zakresie [−1, 1], co pozwala uniezależnić analizę od dziedziny badanych zmiennych.
Poziomy korelacji i ich interpretacja
edytuj| Korelacje | Ujemne | Dodatnie |
|---|---|---|
| Słabe | −0,5 do 0,0 | 0,0 do 0,5 |
| Silne | −1,0 do −0,5 | 0,5 do 1,0 |
Korelacje można interpretować jako silne, słabe, ujemne[1][2]. Interpretacja taka jest jednak arbitralna i nie możemy jej traktować zbyt ściśle. Na przykład współczynnik równy 0,9 dla socjologów i ekonomistów oznacza silną korelację, a dla fizyków posługujących się wysokiej klasy pomiarami przy badaniu praw przyrody oznacza korelację słabą[2]. Z drugiej strony poziom korelacji ma wpływ na czas życia korelacji[1].
Ograniczenia stosowalności
edytuj- podatny na obserwacje skrajne.
- interpretacja jest oczywista tylko dla wielowymiarowego rozkładu normalnego (jest wtedy estymatorem elementu macierzy współczynników tego rozkładu).
Zobacz też
edytujPrzypisy
edytuj- ↑ a b A. Buda, A. Jarynowski (2010), Life-time of correlations and its applications vol. 1, Wydawnictwo Niezależne: 5–21, December 2010, ISBN 978-83-915272-9-0.
- ↑ a b Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.).