Amplituda
Amplituda – największe wychylenie z położenia równowagi w ruchu drgającym i w ruchu falowym. Jednostka amplitudy zależy od rodzaju ruchu drgającego: dla drgań mechanicznych jednostką może być metr, jednostka gęstości lub ciśnienia (np. dla fali podłużnej); dla fali elektromagnetycznej tą jednostką jest V/m.
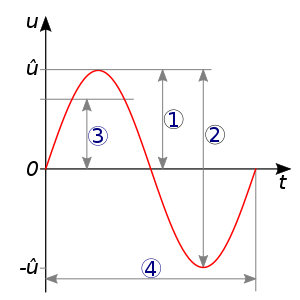
W formalnym opisie drgań amplituda jest liczbą nieujemną określająca wielkość przebiegu funkcji okresowej.
Amplituda w przebiegach sinusoidalnych jest maksymalną wartością tego przebiegu:
- (1)
W przypadku funkcji ze składową stałą, amplituda dotyczy tylko części sinusoidalnej:
- (2)
Amplitudą w tym przypadku nie jest a tylko wartość
Często spotykane błędy w definiowaniu amplitudy
edytujPojęcie amplitudy często jest mylnie określane jako różnica pomiędzy maksymalną a minimalną wartością przebiegu (czyli według tej definicji wynosiłaby – jest to amplituda szczytowo-siodłowa[1]).
Nieprawdziwe jest również definiowanie amplitudy jako wartości średniej z modułów maksymalnej i minimalnej wartości przebiegu (czyli ); taka definicja jest słuszna jedynie dla przebiegów symetrycznych np. sinusoidalnego z równania (1), gdyż wówczas
W meteorologii i klimatologii
edytujW tym przypadku pojęcie amplitudy stosuje się do opisu zjawisk, które nie mają ściśle okresowego charakteru. Amplituda jest wówczas różnicą między maksymalnymi i minimalnymi wartościami liczb charakteryzujących przebieg jakiegoś parametru pogody w odniesieniu do badanego okresu (doby, miesiąca, roku itd.). Pojęcie to odnosi się również do wahań wartości średnich w badanym okresie. Parametrami, których zmienność charakteryzują amplitudy dobowe, miesięczne, roczne są m.in.: temperatura, ciśnienie, wilgotność, nasłonecznienie, ilość opadów itd.
Zobacz też
edytujPrzypisy
edytuj- ↑ International Electrotechnical Commission: Electropedia: peak-to-valley value. [dostęp 2014-11-18].




