Graniastosłup
bryła geometryczna
Graniastosłup – wielościan spełniający dwa warunki[1][2]:
- jego wszystkie wierzchołki są położone na dwóch równoległych płaszczyznach;
- wszystkie krawędzie spoza tych płaszczyzn są do siebie równoległe.

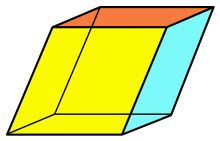
Równoważnie: wielościan, którego dwie ściany są przystające i leżą na dwóch równoległych płaszczyznach, a pozostałe ściany są równoległobokami[3].
Dwie równoległe ściany są znane jako podstawy, a pozostałe jako ściany boczne[a]. Wśród podstaw czasem umownie wyróżnia się górną i dolną[potrzebny przypis].
Jeśli podstawa ma boków, to graniastosłup nazwa się -kątnym[2] i ma on:
- wierzchołków,
- krawędzi,
- ścian.
Pojęcia związane edytuj
- Krawędź boczna – każda krawędź, która nie jest krawędzią podstawy
- Wysokość graniastosłupa – odległość między płaszczyznami podstaw. Niekiedy krótko, ale niezbyt ściśle określa się ją jako odległość między podstawami[b].
- przekątna graniastosłupa – odcinek łączący pewien wierzchołek górnej podstawy z wierzchołkiem dolnej podstawy i nie leżący w żadnej ścianie bocznej ani niebędący krawędzią boczną[c].
Podział i uogólnienia edytuj
- Graniastosłup prosty ma krawędzie boczne prostopadłe do podstawy. Pozostałe graniastosłupy nazywa się pochyłymi[2].
- Graniastosłup prawidłowy jest prosty, a jego podstawy są foremne.
- Graniastosłup archimedesowy – czasem nazywany pryzmą[potrzebny przypis] – jest prawidłowy, a krawędzie jego podstaw są równie długie co wysokość. Graniastosłupy archimedesowe tworzą obok antygraniastosłupów jedną z dwóch nieskończonych serii wielościanów półforemnych.
- Z graniastosłupa przeciętego odpowiednią płaszczyzną można utworzyć graniastosłup ścięty[4].
Wzory edytuj
Przyjęte oznaczenia
- – pole powierzchni podstawy
- – wysokość graniastosłupa.
- – pole powierzchni ścian bocznych.
- Objętość graniastosłupa
- Pole powierzchni graniastosłupa[5]
Uwagi edytuj
- ↑ W przypadku równoległościanu podział na podstawy i ściany boczne jest umowny
- ↑ Takie ujęcie jest poprawne, jeśli rzut prostopadły górnej podstawy na płaszczyznę dolnej podstawy ma z tą dolną podstawą punkty wspólne.
- ↑ graniastosłupy trójkątne nie mają żadnych przekątnych
Przypisy edytuj
- ↑ Encyklopedia Szkolna. Matematyka. Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1988. ISBN 83-02-02551-8. str 75
- ↑ a b c graniastosłup, [w:] Encyklopedia PWN [dostęp 2021-10-10].
- ↑ Encyklopedia dla wszystkich. Matematyka. Warszawa: Wydawnictwo Naukowo-Techniczne, 2000. ISBN 83-204-2334-1. str 108
- ↑ graniastosłup ścięty, [w:] Encyklopedia PWN [dostęp 2021-10-14].
- ↑ Deventhal Katja Maria: Matematyka: kompendium: wzory i reguły, liczne przykłady z rozwiązaniami, od elementarnych działań do matematyki wyższej. Warszawa: Horyzont, 2002, s. 411. ISBN 83-7311-521-8.



