Okrąg opisany na wielokącie

Okrąg opisany na wielokącie – okrąg, na którym leżą wszystkie wierzchołki wielokąta.

Wpisany w okrąg wielokąt z zaznaczonymi symetralnymi.

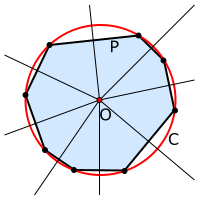
Na wielokącie można opisać okrąg wtedy i tylko wtedy, gdy symetralne jego wszystkich boków przecinają się w jednym punkcie. Punkt ten jest wówczas środkiem okręgu opisanego. Wynika stąd, że na żadnym wielokącie niewypukłym nie da się opisać okręgu. Również nie na każdym wielokącie wypukłym można go opisać. Można to jednak zrobić dla każdego trójkąta, prostokąta oraz wielokąta foremnego.

Okrąg opisany na trójkącie

Okrąg można opisać na każdym trójkącie. Długość promienia okręgu opisanego na trójkącie o bokach równych odpowiednio $a,$ $b,$ $c$ wynosi:

$R={\frac {1}{4P}}abc$ (gdzie $P$ jest polem trójkąta).

Promień możemy wyznaczyć też z twierdzenia sinusów, ze wzoru:

$2R={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}.$

Przykład

Wystarczy znać długość boku i leżącego naprzeciwko niego kąta, np. mając dane $a$ i $\alpha$ obliczamy

$R={\frac {a}{2\sin \alpha }}.$

Promień okręgu opisanego na trójkącie prostokątnym jest równy $c/2.$ Przeciwprostokątna $c$ jest zarazem średnicą tego okręgu, a kąt prosty trójkąta – oparty na średnicy.

Z kolei w przypadku trójkąta równobocznego o boku $a$ stosuje się wzór:

$R={\frac {a}{2\sin {\frac {\pi }{3}}}}={\frac {a{\sqrt {3}}}{3}}.$

Twierdzenie o okręgu opisanym na czworokącie

Okrąg opisany na czworokącie

Twierdzenie. Okrąg można opisać na czworokącie wtedy i tylko wtedy, gdy sumy przeciwległych kątów są równe $\pi .$

$\alpha +\beta =\gamma +\delta =\pi .$

Dowód

Kąty $\alpha$ i $\alpha '$ oraz $\beta$ i $\beta '$ są parami kątów opartych na tym samym łuku. Na mocy twierdzenia o kącie wpisanym i kącie środkowym opartych na tym samym łuku otrzymujemy następujące zależności:

$\alpha '=2\alpha ,$

$\beta '=2\beta .$

Jednocześnie kąty $\alpha '$ i $\beta '$ tworzą razem kąt pełny. Zatem:

$\alpha '+\beta '=2\pi ,$

$2\alpha +2\beta =2\pi ,$

$\alpha +\beta =\pi .$

Analogicznie postępujemy dla drugiej pary kątów.

Przypuśćmy przeciwnie, że na czworokącie $ABCD$ nie można opisać okręgu. Środek okręgu opisanego na trójkącie $ABC$ oznaczmy przez $O.$ Wówczas albo: suma kątów $OAD$ i $OCD$ jest większa lub równa $\pi ,$ albo przynajmniej jedna z półprostych otwartych $AD,$ $CD$ przecina łuk $AC$ (bo jeden z kątów $OAD,$ $OCD$ jest mniejszy niż ${\frac {\pi }{2}}$).

W pierwszym przypadku ze względu na sumę kątów w czworokącie kąt $ADC$ byłby mniejszy bądź równy $\pi -2\angle ABC$ i suma jego i kąta $ABC$ byłaby mniejsza niż $\pi .$

W drugim przypadku bez zmniejszenia ogólności można założyć, że półprosta $AD$ przecina okrąg w punkcie $D'.$ Ale wtedy z udowodnionej części twierdzenia zachodzi $\angle ABC+\angle AD'C=\pi$ i jeśli założyć, że spełniony jest warunek $\angle ABC+\angle ADC=\pi ,$ to będzie z niego wynikać równość kątów $ADC$ i $AD'C.$ Następnie ze współliniowości $A,$ $D$ i $D'$ oraz twierdzenia Talesa równoległość $DC$ i $D'C$ sprzeczna z tym, że się przecinają.

Zobacz też

• okrąg wpisany w wielokąt
• kula opisana