Twierdzenie Rolle’a

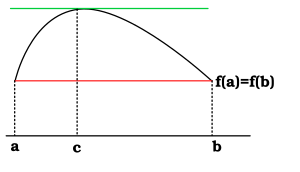
Twierdzenie Rolle’a – twierdzenie klasycznej analizy matematycznej mówiące, że funkcja różniczkowalna przyjmująca równe wartości w dwóch różnych punktach ma pomiędzy nimi punkt stacjonarny, tzn. punkt, w którym nachylenie prostej stycznej do wykresu funkcji względem osi OX jest równe zeru. Jest to najprostszy przypadek twierdzenia Lagrange’a o wartości średniej, a przez to – twierdzenia Cauchy’ego. Jest używane m.in. w dowodzie reguły znaków Kartezjusza.

Ilustracja twierdzenia

Twierdzenie to – w innej postaci niż ta standardowa – znał w 1150 roku indyjski matematyk Bhaskaraćarja. W 1691 roku francuski matematyk Michel Rolle opublikował je w szczególnym przypadku dotyczącym wielomianów. Zostało nazwane na jego cześć najpóźniej w XIX wieku; nazwiskiem Rolle’a określił je w 1834 roku Moritz Wilhelm Drobisch.

Wersja standardowa

Niech $f$ będzie ciągłą funkcją rzeczywistą określoną na przedziale domkniętym $[a,b],$ różniczkowalną na przedziale otwartym $(a,b).$ Wówczas jeżeli $f(a)=f(b),$ to istnieje taki punkt $c$ należący do przedziału otwartego $(a,b),$ że

$f'(c)=0.$

Z tej wersji twierdzenia Rolle’a korzysta się przy dowodzie twierdzenia Lagrange’a o wartości średniej, którego twierdzenie Rolle’a jest przypadkiem szczególnym.

Dowód

Wizualizacja graficzna twierdzenia

Jeżeli $f\equiv \mathrm {const} ,$ to $f'(c)=0$ dla każdego $c\in (a,b).$ Gdy $f$ nie jest tożsamościowo równa stałej, to istnieje taki punkt $x\in (a,b),$ dla którego zachodzi

$f(x)>f(a)=f(b)$

lub

$f(x)<f(a)=f(b).$

Przypuśćmy, że zachodzi pierwszy przypadek, tzn. dla pewnego argumentu wartość funkcji jest większa od $f(a)=f(b);$ rozumowanie w drugim przypadku jest analogiczne (wówczas trzeba rozważać wartość najmniejszą zamiast największej).

Określona na przedziale zwartym $[a,b]$ funkcja ciągła $f$ na mocy twierdzenia Weierstrassa przyjmuje wartość największą, tzn. istnieje taki punkt $c\in [a,b],$ że

$f(c)=\sup f(x)$

dla $x\in [a,b].$

Z założenia, że istnieje wartość większa od $f(a)=f(b)$ wynika, że $a\neq c\neq b,$ tzn. $c\in (a,b).$ Warunkiem koniecznym istnienia ekstremum globalnego funkcji $f$ w $c$ jest znikanie pochodnej w tym punkcie, co dowodzi tezy.

Uogólnienia

Niech $h:=b-a$ będzie rzeczywistą liczbą dodatnią, a $x:=a,$ wtedy $x+h=b.$ Punkt $c\in (a,b)$ można zapisać jako $x+\theta h,$ gdzie $\theta \in (0,1).$

Przy takich oznaczeniach twierdzenie Rolle’a ma postać:

Jeśli

$f(x+h)=f(x),$

to istnieje punkt $x+\theta h,$ dla którego

$f'(x+\theta h)h=0.$

Rezygnacja z warunku $f(a)=f(b),$ czyli $f(x)=f(x+h),$ prowadzi do ogólniejszego twierdzenia Lagrange’a:

Istnieje taki punkt $x+\theta h,$ który spełnia tożsamość

$f(x+h)=f(x)+f'(x+\theta h)h.$

Z kolei dalekim uogólnieniem twierdzenia Lagrange’a jest twierdzenie Taylora mówiące, że:

Istnieje taki punkt $x+\theta h,$ dla którego zachodzi:

$f(x+h)={\frac {f^{(0)}(x)}{0!}}h^{0}+{\frac {f'(x)}{1!}}h^{1}+{\frac {f^{(2)}(x)}{2!}}h^{2}+\dots +{\frac {f^{(n)}(x)}{n!}}h^{n}+{\frac {f^{(n+1)}(x+\theta h)}{(n+1)!}}h^{n+1},$

gdzie o funkcji $f$ zakłada się, by była $n+1$ razy różniczkowalna.

Twierdzenie Rolle’a uzyskuje się z niego przyjmując $n=0.$

Zobacz też

• twierdzenie Darboux

Bibliografia

• G.M. Fichtenholz: Rachunek różniczkowy i całkowy. Wyd. dwunaste. T. 1. Warszawa: Wydawnictwo Naukowe PWN, 2002, s. 195. ISBN 83-01-02175-6.

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Rolle's Theorem, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2022-06-20].
• Rolle theorem (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2022-06-20].
• William L. Hosch, Rolle’s theorem (ang.), Encyklopedia Britannica, britannica.com [dostęp 2023-06-06].