Funkcja Γ

Funkcja gamma (zwana też funkcją gamma Eulera) – funkcja specjalna, która rozszerza pojęcie silni na zbiór liczb rzeczywistych i zespolonych.

Wykres funkcji gamma

Czy istnieją inne funkcje niż funkcja gamma, które interpolują funkcję silnia dla dowolnych liczb rzeczywistych?

Definicje

Całkowa

Jeżeli $x$ – część rzeczywista liczby zespolonej $z=x+iy$ jest dodatnia, to

$\Gamma (z)=\int \limits _{0}^{+\infty }t^{z-1}\,e^{-t}\,dt,\quad x>0$

– tzw. całka Eulera 2 rodzaju (całka Eulera 1 rodzaju – to funkcja Beta)

Iloczynowa

Dla dowolnych liczb zespolonych $z=x+iy$ mamy

$\Gamma (z)=\lim _{n\to +\infty }{\frac {n!n^{z}}{z(z+1)(z+2)\dots (z+n)}}={\frac {1}{z}}\prod _{n=1}^{\infty }{\frac {\left(1+{\frac {1}{n}}\right)^{z}}{1+{\frac {z}{n}}}}.$

Motywacja

Funkcja gamma może być postrzegana jako rozwiązanie następującego problemu interpolacji:

„Znajdź gładką krzywą, która łączy punkty $(x,y)$ dane przez funkcję $y=(x-1)!,$ która jest określona dla dodatnich liczb całkowitych $x$”.

Wzór $x!=1\cdot 2\dots x$ nie może być użyty dla niecałkowitych wartości $x,$ ponieważ jest ważny tylko wtedy, gdy $x$ jest liczbą naturalną.

Funkcja gamma jest dobrym rozwiązaniem, jednak nie jest to jedyne rozwiązanie: istnieje bowiem nieskończenie wiele ciągłych rozszerzeń funkcji silnia na liczby niecałkowite, gdyż przez zbiór izolowanych punktów (jaki tworzy wykres funkcji silnia) można narysować nieskończenie wiele różnych krzywych.

Funkcja gamma jest najbardziej użytecznym rozwiązaniem w praktyce, ponieważ jest funkcją analityczną (z wyjątkiem niedodatnich liczb całkowitych) i można ją zdefiniować na kilka równoważnych sposobów.

Nie jest to także jedyna funkcja analityczna, która rozszerza silnię, ponieważ dodanie do niej dowolnej funkcji analitycznej, która zeruje się dla dodatnich liczb całkowitych, takich jak ${\text{k sin}}(m\pi x),$ gdzie $m$ – liczba całkowita, da inną funkcję interpolującą silnię. Takie funkcje nazywa się funkcjami pseudogamma. Najbardziej znaną jest funkcja Hadamarda.

Własności funkcji Gamma

Dwa dobre uogólnienia analityczne funkcji silnia na zbiór liczb rzeczywistych: funkcja $\Gamma (z)$ – wykres niebieski oraz funkcja $\Gamma (z)+sin(\pi \cdot z)$ – wykres zielony. Obie te funkcje przecinają się dla liczb naturalnych.

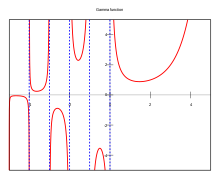
Tw. Funkcja gamma nie ma miejsc zerowych (por. wykres)

Tw. $\Gamma (1)=1$

Tw. $\Gamma (n+1)=n!\quad {\text{dla}}\quad n\in N$,

gdzie $N$ – zbiór liczb naturalnych,

tzn. funkcja gamma ma wartości identyczne jak silnia dla liczb naturalnych.

Tw. Dla $n\in N$ mamy

$\Gamma \left(n+{\frac {1}{2}}\right)={\frac {(2n-1)!!}{2^{n}}}{\sqrt {\pi }}$

$\Gamma (n+1/p)=\Gamma (1/p){\frac {(pn-(p-1))!^{(p)}}{p^{n}}}$

gdzie $x!^{(p)}$ oznacza tzw. silnię wielokrotną p-tą.

Tw. $\Gamma (z+1)=z\cdot \Gamma (z)$

Dowód – metodą całkowania przez części.

Tw. $\Gamma (z)\cdot \Gamma \left(z+{\frac {1}{2}}\right)={\frac {\sqrt {\pi }}{2^{2\cdot z\ -1}}}\cdot \Gamma (2z)$

Tw. Jeżeli mianownik jest niezerowy, to:

$\Gamma (z)\cdot \Gamma (1-z)={\frac {\pi }{\sin {\pi z}}},$

$\Gamma \left(z+{\frac {1}{2}}\right)\cdot \Gamma \left({\frac {1}{2}}-z\right)={\frac {\pi }{\cos {\pi z}}}.$

Tw. Jeśli $-1<\operatorname {Re} (z)<1,$ to:

$\Gamma (z)={\frac {1}{\sin {{\frac {\pi }{2}}z}}}\int _{0}^{\infty }t^{z-1}\sin {t}\,dt.$

Tw. Jeśli $0<\operatorname {Re} (z)<1,$ to:

$\Gamma (z)={\frac {1}{\cos {{\frac {\pi }{2}}z}}}\int _{0}^{\infty }t^{z-1}\cos {t}\,dt.$

Tw. Wzór iloczynowy Gaussa:

$\Gamma (nz)={\frac {n^{nz}}{\sqrt {(2\pi )^{n-1}}}}\cdot \Gamma (z)\cdot \Gamma \left(z+{\frac {1}{n}}\right)\cdot \Gamma \left(z+{\frac {2}{n}}\right)\cdot \ldots \cdot \Gamma \left(z+{\frac {n-1}{n}}\right).$

Wybrane wartości funkcji Gamma

Tabela wartości funkcji gamma

$x$	$\Gamma (x)$
−2,500	$\approx -0{,}945309$
−2	$\pm \infty$
−1,500	${\frac {4{\sqrt {\pi }}}{3}}\approx 2{,}363271801$
−1	$\pm \infty$
−0,500	$-2{\sqrt {\pi }}\approx -3{,}544907702$
0	$\pm \infty$
0,143	$\approx 6{,}548062940$
0,167	$\approx 5{,}566316002$
0,200	$\approx 4{,}590843712$
0,250	$\approx 3{,}625609908$
0,333	$\approx 2{,}678938535$
0,500	${\sqrt {\pi }}\approx 1{,}772453851$
1	0! = 1
$x_{min}$	$0{,}885603194$
1,500	${\frac {\sqrt {\pi }}{2}}\approx 0{,}886226925$
2	1! = 1
2,500	${\frac {3{\sqrt {\pi }}}{4}}\approx 1{,}329340388$
3	2! = 2
3,500	${\frac {15{\sqrt {\pi }}}{8}}\approx 3{,}323350970$
4	3! = 6

Dla $x_{min}\approx 1{,}461632145$ funkcja $\Gamma (z)$ ma minimum lokalne - jest to jedyne minimum dla liczb $z$, takich że $x=Re\,z>0$; dla $x>x_{min}$ moduł funkcji $\Gamma (z)$ rośnie nieograniczenie do $+\infty$.

Funkcja $\Gamma (z)$ nie jest określona dla $z=0,-1,-2,\dots$ – ma tam bieguny o residuum $(-1)^{z}/z!.$

Wykres funkcji zespolonej – techniki wizualizacji

Wykres funkcji rzeczywistej $y=f(x)$ można narysować w 2 wymiarach. Wykres funkcji zespolonej, mającej zarówno zespoloną dziedzinę, jak i zespolony zbiór wartości, wymagałby 4 wymiarów. Jednym ze sposobów rozwiązania tego problemu jest metoda wizualizacji za pomocą powierzchni Riemanna; inną metodą jest technika kolorowanie dziedziny.

Wykres funkcji zespolonej $\Gamma (z){:}$ oś x – części rzeczywiste liczb zespolonych postaci $z=x+iy,$ oś y – części urojone tych liczb, oś z – $|\Gamma (z)|,$ tj. moduł funkcji gamma; kolor – zależy od $arg\,\Gamma (z),$ tj. od wartości argumentu funkcji gamma.

Kompletny wykres

Moduł

Argument

Część rzeczywista

Część urojona

Wykres funkcji zespolonej $\Gamma (z)$ uzyskany techniką kolorowania dziedziny

Odwrotność funkcji gamma

${\frac {1}{\Gamma (z)}}=ze^{\gamma z}\prod _{n=1}^{\infty }\left[\left(1+{\frac {z}{n}}\right)e^{-{\frac {z}{n}}}\right]$

gdzie γ to stała Eulera-Mascheroniego.

Odwrotność funkcji gamma jest określona na całej płaszczyźnie zespolonej, gdyż funkcja $\Gamma (z)$ nie ma miejsc zerowych – taką funkcję nazywa się funkcją całkowitą.

Logarytmiczna pochodna funkcji gamma

Wykres logarytmicznej pochodnej funkcji gamma

Df. Logarytmiczną pochodną funkcji gamma albo funkcją di-gamma nazywa się funkcję postaci

$\psi (z)={\frac {\Gamma '(z)}{\Gamma (z)}},$

gdzie $z\neq 0,-1,-2,\dots$

Tw. $\psi (z)=-\gamma +\sum _{n=0}^{\infty }\left({\frac {1}{n+1}}-{\frac {1}{n+z}}\right),$

gdzie $\gamma$ – stała Eulera-Mascheroniego

Tw. $\psi '(z)=\sum _{k=0}^{\infty }{\frac {1}{\left(z+k\right)^{2}}}.$

Tw. Dla $x>>1$ słuszne jest przybliżenie:

$\psi (x)\approx \ln x-{\frac {1}{2x}}.$

Funkcja poligamma

Df. Funkcją poligamma n-tego rzędu nazywamy $n+1$-szą pochodną funkcji $\ln \Gamma (z),$ tj.

$\psi ^{(n)}(z)={\frac {d^{n}\psi (z)}{dz^{n}}}=\left({\frac {d}{dz}}\right)^{n+1}\ln \Gamma (z),$

Wtedy:

$\psi (z)=\psi ^{(0)}(z).$

Df. Funkcją tri-gamma (lub trój-gamma) nazywa się funkcją $\psi ^{(1)}.$

Funkcja $\ln \Gamma (z)$ i kilka pierwszych funkcji poligamma na płaszczyźnie zespolonej

$\ln \Gamma (z)$

$\psi ^{(0)}(z)$ (digamma)

$\psi ^{(1)}(z)$ (trigamma)

$\psi ^{(2)}(z)$

$\psi ^{(3)}(z)$

$\psi ^{(4)}(z)$

Wykresy funkcji zespolonej uzyskane techniką kolorowania dziedziny

Zastosowania funkcji gamma

Funkcja gamma ma ogromnie liczne zastosowania (sekcja wymaga rozwinięcia)

• Na funkcji gamma opiera się symbol Pochhammera.
• Wzór na objętość n-wymiarowej hipersfery: $S_{n}=(2*\pi ^{n/2})/(\Gamma (1/2n))$.

Zobacz też

• funkcja beta
• funkcje specjalne

Bibliografia

• I. N. Bronsztejn, K. A. Siemiendiajew, Poradnik encyklopedyczny. Matematyka, Wydawnictwo Naukowe PWN, Warszawa 2010, s. 192–193.

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Gamma Function, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).
• Wykres modułu z funkcji Gamma w zespolonych. mathworks.com. [zarchiwizowane z tego adresu (2009-12-20)].

Kalkulator online:

• Kalkulator funkcji gamma online https://keisan.casio.com/exec/system/1180573451
• Kalkulator odwrotnej funkcji gamma online https://keisan.casio.com/exec/system/1180573451
• Kalkulator funkcji ln gamma online https://keisan.casio.com/exec/system/1180573451