Walec (bryła)
Walec jest bryłą geometryczną ograniczoną powierzchnią walcową i dwiema płaszczyznami nierównoległymi do jej tworzącej. Jeżeli płaszczyzny są prostopadłe do tworzącej, wówczas jest to walec prosty. Czasem definicja walca jest zawężona tylko do tego szczególnego przypadku – podstaw prostopadłych do powierzchni bocznej[1].
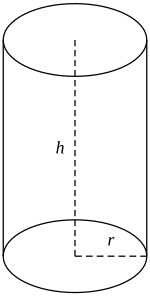
Walec kołowy prosty jest bryłą geometryczną powstałą w wyniku obrotu prostokąta wokół jednego z jego boków. Podstawą walca oraz jego górną częścią jest koło, a jego szerokość jest w każdym miejscu taka sama.
Bryła ta jest w pewnym kartezjańskim układzie współrzędnych opisana jako zbiór punktów spełniających układ nierówności:
zaś w pewnym układzie walcowym jako zbiór punktów spełniających układ nierówności:
gdzie jest promieniem walca, zaś – jego wysokością.
Często walcem nazywa się też powierzchnię walcową, będącą przedłużeniem w nieskończoność powierzchni bocznej walca. Jej równanie: Prosta przesuwającą się równolegle wzdłuż krzywej płaskiej (podstawy walca), która zakreśla powierzchnię walcową, nazywa się tworzącą walca.
Walcami określa się również inne bryły i powierzchnie, których podstawą może być jakakolwiek figura płaska. Najczęściej rozpatruje się przypadek, kiedy tą podstawą jest krzywa stożkowa: elipsa, hiperbola, lub parabola. Mówimy wówczas odpowiednio o walcu eliptycznym, hiperbolicznym i parabolicznym, przy czym jedynie pierwszy z nich może stanowić bryłę, a pozostałe dwa są powierzchniami nieskończonymi.
Podstawowe wzory edytuj
Niech:
- – promień podstawy walca,
- – wysokość walca.
Wzór na pole powierzchni podstawy walca kołowego prostego:
Wzór na pole powierzchni bocznej walca kołowego prostego:
Wzór na pole powierzchni całkowitej walca kołowego prostego:
Wzór na objętość walca kołowego prostego:
Zobacz też edytuj
Przypisy edytuj
- ↑ walec, [w:] Encyklopedia PWN [dostęp 2021-10-09].
- ↑ a b c Wybrane wzory matematyczne, Warszawa: Centralna Komisja Egzaminacyjna, 2015, s. 14, ISBN 978-83-940902-1-0.






